- Derivative Of Arctangent
- Derivative Of Arcsin
- Derivative Of Arccos
- Derivative Of Arctan U
- Derivative Of Arctan(y/x)
- How to differentiate arctan x.
- Assuming we know the derivative of tan(x) is sec 2 (x): Let y = arctan(x) so that x = tan(y). Differentiate both sides with respect to x to get: 1 = sec 2 (y) dy/dx. Now use the identity. Sin 2 (y) + cos 2 (y) = 1. Divide by cos 2 (y) to get. Tan 2 (y) + 1 = sec 2 (y) Use the substitution tan(y) = x to get. Sec 2 (y) = 1 + x 2.
- Find the Derivative - d/dx y=arctan(1/x) Differentiate using the chain rule, which states that is where. Tap for more steps. To apply the Chain Rule, set as.
In the following discussion and solutions the derivative of a function h(x) will be denoted by or h'(x). The derivatives of the above-mentioned inverse trigonometric functions follow from trigonometry identities, implicit differentiation, and the chain rule. Below is shown arctan(tan(x)) in red and its derivative in blue. Note that the derivative is undefined for values of x for which cos(x) is equal to 0, which means at x = π/2 + k. π, where k is an integer.
The inverse hyperbolic tangent (Zwillinger 1995, p. 481; Beyer 1987, p. 181), sometimes called the area hyperbolic tangent (Harris and Stocker 1998, p. 267), is the multivalued function that is the inverse function of the hyperbolic tangent.
The function is sometimes denoted (Jeffrey 2000, p. 124) or (Gradshteyn and Ryzhik 2000, p. xxx). The variants or (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse hyperbolic tangent, although this distinction is not always made. Worse yet, the notation is sometimes used for the principal value, with being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). Note that in the notation , is the hyperbolic tangent and the superscript denotes an inverse function, not the multiplicative inverse.
The principal value of is implemented in the Wolfram Language as ArcTanh[z] and in the GNU C library as atanh(double x).
The inverse hyperbolic tangent is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segments and . This follows from the definition of as
The inverse hyperbolic tangent is given in terms of the inversetangent by
(Gradshteyn and Ryzhik 2000, p. xxx). For real , this simplifies to
The derivative of the inverse hyperbolic tangent is
and the indefinite integral is
It has special values
(6) |
(8) |
It has Maclaurin series
(10) |
(12) |
(OEIS A005408).
An indefinite integral involving is given by
(14) |
(16) |
when .
SEE ALSO:Hyperbolic Tangent, Inverse Hyperbolic Cotangent, Inverse Hyperbolic FunctionsRELATED WOLFRAM SITES:https://functions.wolfram.com/ElementaryFunctions/ArcTanh/
REFERENCES:Abramowitz, M. and Stegun, I. A. (Eds.). 'Inverse Hyperbolic Functions.' §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
GNU C Library. 'Mathematics: Inverse Trigonometric Functions.' https://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.
Harris, J. W. and Stocker, H. Handbookof Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Jeffrey, A. 'Inverse Trigonometric and Hyperbolic Functions.' §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.
Sloane, N. J. A. Sequence A005408/M2400in 'The On-Line Encyclopedia of Integer Sequences.'
Spanier, J. and Oldham, K. B. 'Inverse Trigonometric Functions.' Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Zwillinger, D. (Ed.). 'Inverse Hyperbolic Functions.' §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.
Referenced on Wolfram|Alpha: Inverse Hyperbolic TangentCITE THIS AS:Weisstein, Eric W. 'Inverse Hyperbolic Tangent.'From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/InverseHyperbolicTangent.html
 Show Mobile NoticeShow All NotesHide All Notes
Show Mobile NoticeShow All NotesHide All NotesSection 3-7 : Derivatives of Inverse Trig Functions

In this section we are going to look at the derivatives of the inverse trig functions. In order to derive the derivatives of inverse trig functions we’ll need the formula from the last section relating the derivatives of inverse functions. If (fleft( x right)) and (gleft( x right)) are inverse functions then,
[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}}]Recall as well that two functions are inverses if (fleft( {gleft( x right)} right) = x) and (gleft( {fleft( x right)} right) = x).
We’ll go through inverse sine, inverse cosine and inverse tangent in detail here and leave the other three to you to derive if you’d like to.
Inverse Sine
Let’s start with inverse sine. Here is the definition of the inverse sine.
[y = {sin ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}sin y = xhspace{0.25in}{mbox{for}}, - frac{pi }{2} le y le frac{pi }{2}]So, evaluating an inverse trig function is the same as asking what angle (i.e. (y)) did we plug into the sine function to get (x). The restrictions on (y) given above are there to make sure that we get a consistent answer out of the inverse sine. We know that there are in fact an infinite number of angles that will work and we want a consistent value when we work with inverse sine. Using the range of angles above gives all possible values of the sine function exactly once. If you’re not sure of that sketch out a unit circle and you’ll see that that range of angles (the (y)’s) will cover all possible values of sine.
Note as well that since ( - 1 le sin left( y right) le 1) we also have ( - 1 le x le 1).
Let’s work a quick example.
Example 1 Evaluate (displaystyle {sin ^{ - 1}}left( {frac{1}{2}} right)) Show SolutionSo, we are really asking what angle (y) solves the following equation.
[sin left( y right) = frac{1}{2}]and we are restricted to the values of (y) above.
From a unit circle we can quickly see that (y = frac{pi }{6}).
We have the following relationship between the inverse sine function and the sine function.
[sin left( {{{sin }^{ - 1}}x} right) = xhspace{0.5in}{sin ^{ - 1}}left( {sin x} right) = x]In other words they are inverses of each other. This means that we can use the fact above to find the derivative of inverse sine. Let’s start with,
[fleft( x right) = sin xhspace{0.5in}gleft( x right) = {sin ^{ - 1}}x]Then,
[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{cos left( {{{sin }^{ - 1}}x} right)}}]This is not a very useful formula. Let’s see if we can get a better formula. Let’s start by recalling the definition of the inverse sine function.
[y = {sin ^{ - 1}}left( x right)hspace{0.5in} Rightarrow hspace{0.5in}x = sin left( y right)]Using the first part of this definition the denominator in the derivative becomes,
[cos left( {{{sin }^{ - 1}}x} right) = cos left( y right)]Now, recall that
[{cos ^2}y + {sin ^2}y = 1hspace{0.5in} Rightarrow hspace{0.5in}cos y = sqrt {1 - {{sin }^2}y} ]Using this, the denominator is now,
[cos left( {{{sin }^{ - 1}}x} right) = cos left( y right) = sqrt {1 - {{sin }^2}y} ]Now, use the second part of the definition of the inverse sine function. The denominator is then,
[cos left( {{{sin }^{ - 1}}x} right) = sqrt {1 - {{sin }^2}y} = sqrt {1 - {x^2}} ]Putting all of this together gives the following derivative.
[frac{d}{{dx}}left( {{{sin }^{ - 1}}x} right) = frac{1}{{sqrt {1 - {x^2}} }}]Inverse Cosine
Now let’s take a look at the inverse cosine. Here is the definition for the inverse cosine.
[y = {cos ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}cos y = xhspace{0.25in}{mbox{for}},0 le y le pi ]As with the inverse sine we’ve got a restriction on the angles, (y), that we get out of the inverse cosine function. Again, if you’d like to verify this a quick sketch of a unit circle should convince you that this range will cover all possible values of cosine exactly once. Also, we also have ( - 1 le x le 1) because ( - 1 le cos left( y right) le 1).
Example 2 Evaluate (displaystyle {cos ^{ - 1}}left( { - frac{{sqrt 2 }}{2}} right)). Show SolutionAs with the inverse sine we are really just asking the following.
[cos y = - frac{{sqrt 2 }}{2}]where (y) must meet the requirements given above. From a unit circle we can see that we must have (y = frac{{3pi }}{4}).
The inverse cosine and cosine functions are also inverses of each other and so we have, [cos left( {{{cos }^{ - 1}}x} right) = xhspace{0.5in}{cos ^{ - 1}}left( {cos x} right) = x]To find the derivative we’ll do the same kind of work that we did with the inverse sine above. If we start with
[fleft( x right) = cos xhspace{0.5in}gleft( x right) = {cos ^{ - 1}}x]then,
[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{ - sin left( {{{cos }^{ - 1}}x} right)}}]Simplifying the denominator here is almost identical to the work we did for the inverse sine and so isn’t shown here. Upon simplifying we get the following derivative.
[frac{d}{{dx}}left( {{{cos }^{ - 1}}x} right) = - frac{1}{{sqrt {1 - {x^2}} }}]So, the derivative of the inverse cosine is nearly identical to the derivative of the inverse sine. The only difference is the negative sign.
Inverse Tangent
Here is the definition of the inverse tangent.
[y = {tan ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}tan y = xhspace{0.25in}{mbox{for}}, - frac{pi }{2} < y < frac{pi }{2}]Again, we have a restriction on (y), but notice that we can’t let (y) be either of the two endpoints in the restriction above since tangent isn’t even defined at those two points. To convince yourself that this range will cover all possible values of tangent do a quick sketch of the tangent function and we can see that in this range we do indeed cover all possible values of tangent. Also, in this case there are no restrictions on (x) because tangent can take on all possible values.
Example 3 Evaluate ({tan ^{ - 1}}1). Show SolutionDerivative Of Arctangent
Here we are asking,
[tan y = 1]where (y) satisfies the restrictions given above. From a unit circle we can see that (y = frac{pi }{4}).
Because there is no restriction on (x) we can ask for the limits of the inverse tangent function as (x) goes to plus or minus infinity. To do this we’ll need the graph of the inverse tangent function. This is shown below.
From this graph we can see that
[mathop {lim }limits_{x to infty } {tan ^{ - 1}}x = frac{pi }{2}hspace{0.5in}hspace{0.25in}mathop {lim }limits_{x to - infty } {tan ^{ - 1}}x = - frac{pi }{2}]The tangent and inverse tangent functions are inverse functions so,
[tan left( {{{tan }^{ - 1}}x} right) = xhspace{0.5in}{tan ^{ - 1}}left( {tan x} right) = x]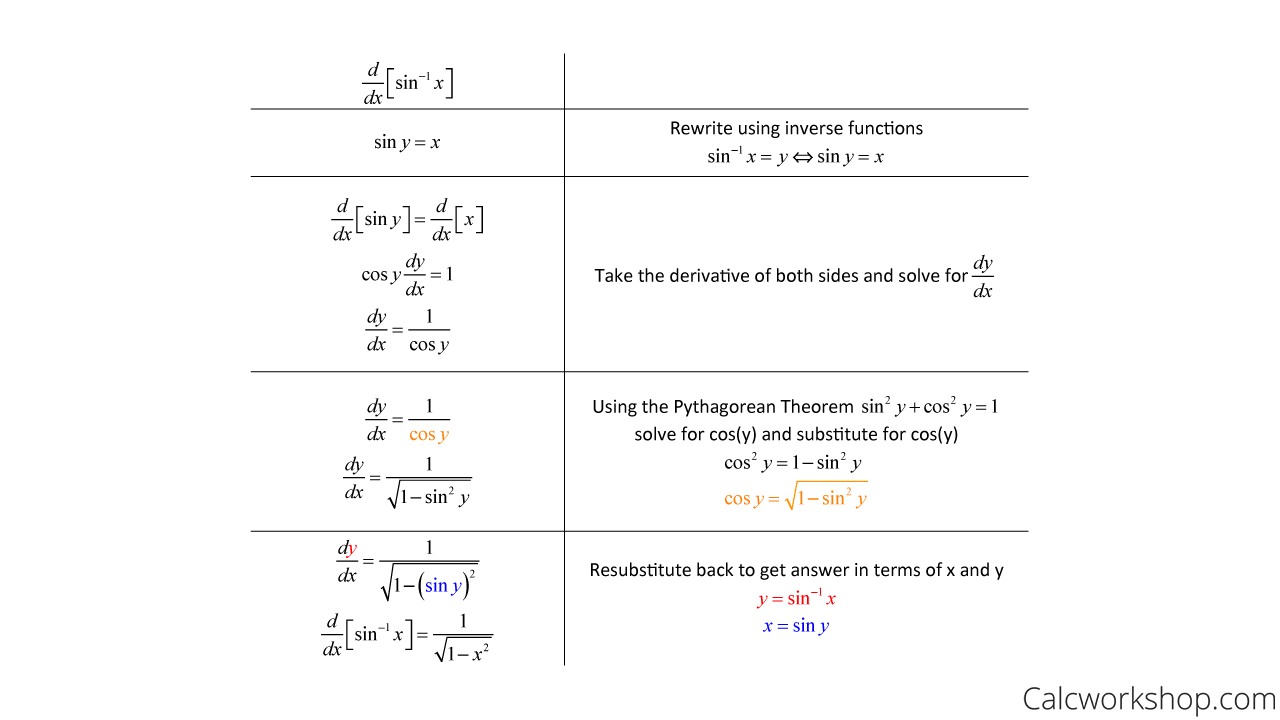
Therefore, to find the derivative of the inverse tangent function we can start with
[fleft( x right) = tan xhspace{0.5in}gleft( x right) = {tan ^{ - 1}}x]We then have,
[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{{{sec }^2}left( {{{tan }^{ - 1}}x} right)}}]Simplifying the denominator is similar to the inverse sine, but different enough to warrant showing the details. We’ll start with the definition of the inverse tangent.
[y = {tan ^{ - 1}}xhspace{0.5in} Rightarrow hspace{0.5in}tan y = x]The denominator is then,
[{sec ^2}left( {{{tan }^{ - 1}}x} right) = {sec ^2}y]Now, if we start with the fact that
[{cos ^2}y + {sin ^2}y = 1]and divide every term by cos2 (y) we will get,
[1 + {tan ^2}y = {sec ^2}y]The denominator is then,
[{sec ^2}left( {{{tan }^{ - 1}}x} right) = {sec ^2}y = 1 + {tan ^2}y]Finally using the second portion of the definition of the inverse tangent function gives us,
[{sec ^2}left( {{{tan }^{ - 1}}x} right) = 1 + {tan ^2}y = 1 + {x^2}]The derivative of the inverse tangent is then,
[frac{d}{{dx}}left( {{{tan }^{ - 1}}x} right) = frac{1}{{1 + {x^2}}}]There are three more inverse trig functions but the three shown here the most common ones. Formulas for the remaining three could be derived by a similar process as we did those above. Here are the derivatives of all six inverse trig functions.
We should probably now do a couple of quick derivatives here before moving on to the next section.
Example 4 Differentiate the following functions.- (fleft( t right) = 4{cos ^{ - 1}}left( t right) - 10{tan ^{ - 1}}left( t right))
- (y = sqrt z , {sin ^{ - 1}}left( z right))
Not much to do with this one other than differentiate each term.
[f'left( t right) = - frac{4}{{sqrt {1 - {t^2}} }} - frac{{10}}{{1 + {t^2}}}]b (y = sqrt z , {sin ^{ - 1}}left( z right)) Show Solution
Don’t forget to convert the radical to fractional exponents before using the product rule.
Derivative Of Arcsin
[y' = frac{1}{2}{z^{ - frac{1}{2}}}{sin ^{ - 1}}left( z right) + frac{{sqrt z }}{{sqrt {1 - {z^2}} }}]Derivative Of Arccos
Alternate Notation
Derivative Of Arctan U
There is some alternate notation that is used on occasion to denote the inverse trig functions. This notation is,