Take on the roles of Alice and Bob! Exchange secret keys using the Diffie-Hellman key exchange method!! Use your keys to encrypt messages!!!
The Diffie-Hellman key exchange algorithm was first published in 1976 by Whitfield Diffie and Martin Hellman, although the algorithm had been invented a few years earlier by the British government intelligence agency GCHQ but was kept classified. The Diffie-Hellman key exchange uses a large prime pand a primitive root gof this prime. These numbers are both public. To start the key exchange process, Alice chooses a secret number aless than the large prime, and computes ga(mod p). Alice sends this answer, call it A, to Bob. Diffie Hellman Calculator - fasrlosangeles.
- Diffie Hellman Algorithm (DH) Diffie Hellman (DH) key exchange algorithm is a method for securely exchanging cryptographic keys over a public communications channel. Keys are not actually exchanged – they are jointly derived. It is named after their inventors Whitfield Diffie and Martin Hellman.
- Recall the mathematics of Diffie-Hellman: Given public. Stack Exchange Network. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
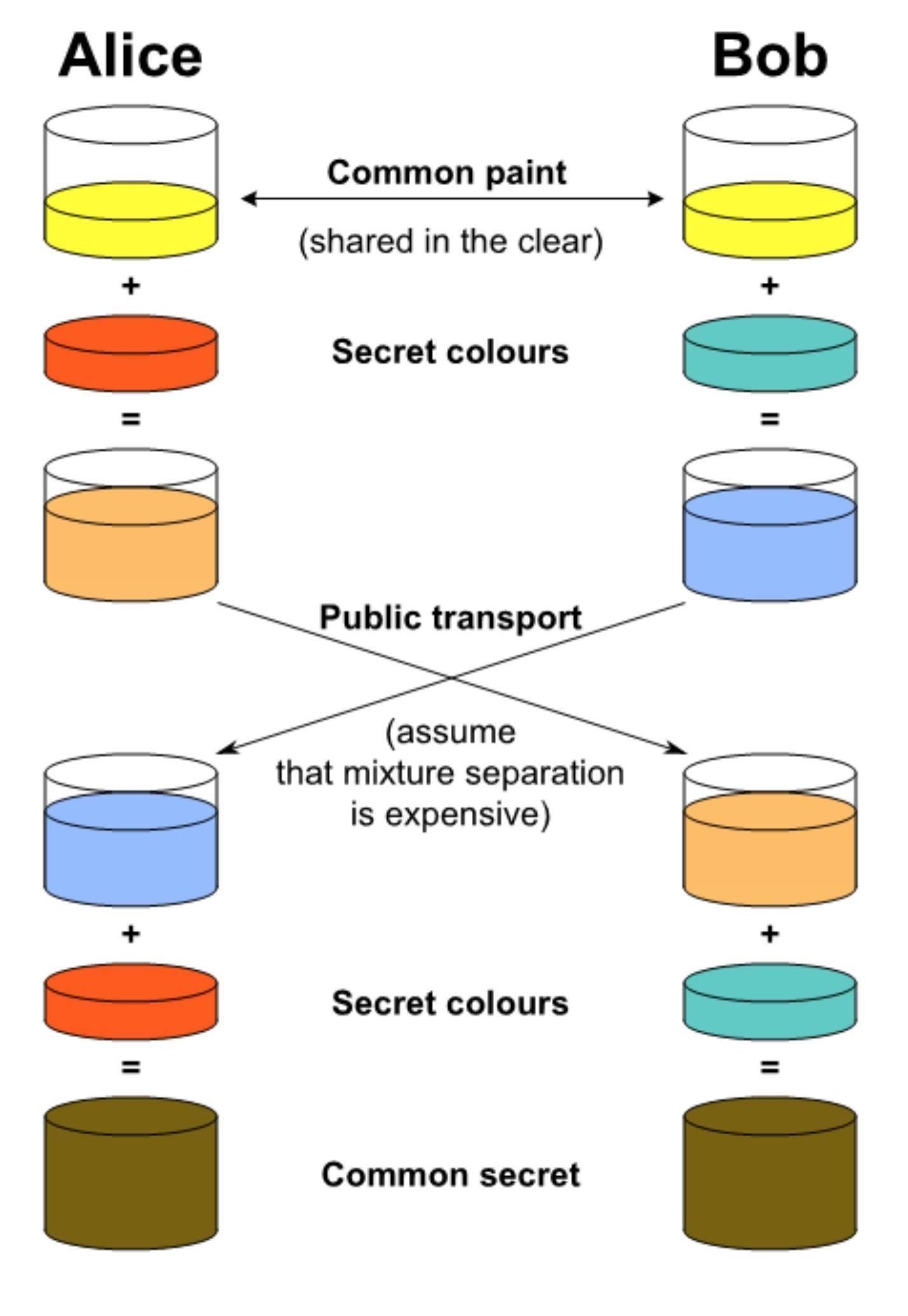
The Diffie-Hellman key exchange uses a large prime p and a primitive root g of this prime. These numbers are both public.
To start the key exchange process, Alice chooses a secret number a less than the large prime, and computes ga (mod p). Alice sends this answer, call it A, to Bob. Bob now chooses his own secret number b, and computes gb (mod p). Bob sends this answer, call it B, to Alice.
Finally, Alice computes Ba (mod p), and Bob computes Ab (mod p). They both get the same answer, but no-one else will know this secret answer, because only Alice knows a, and only Bob knows b. This secret answer is their private key, which they can use to encrypt messages.

[You may wonder why someone intercepting Alice and Bob's communication can't solve gx = A (mod p) to calculate Alice's secret number a. This is a hard problem, known as the discrete logarithm problem. That this is difficult is the strength of this method of key exchange.]

First you must be Alice. Choose a large prime from the list below (or one of your own choice) and a corresponding primitive root of that large prime. Then choose a secret number which is smaller than your large prime.
- 22953686867719691230002707821868552601124472329079 primitive root 11
- 30762542250301270692051460539586166927291732754961 primitive root 7
- 29927402397991286489627837734179186385188296382227 primitive root 2
- 95647806479275528135733781266203904794419563064407 primitive root 5
- 48705091355238882778842909230056712140813460157899 primitive root 6
- 53542885039615245271174355315623704334284773568199 primitive root 3
- 622288097498926496141095869268883999563096063592498055290461 primitive root 2
- 610692533270508750441931226384209856405876657993997547171387 primitive root 2
- 4669523849932130508876392554713407521319117239637943224980015676156491 primitive root 3
- 4906275427767802358357703730938087362176142642699093827933107888253709 primitive root 2
- 18532395500947174450709383384936679868383424444311405679463280782405796233163977 primitive root 5
- 282755483533707287054752184321121345766861480697448703443857012153264407439766013042402571 primitive root 2
[Back] Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications, and uses two numbers (G and N) for the first part of the calculation (of which N must be a prime number):
[Related Lecture] [Tutorial] [Software Tutorial][Software Lecture] [Theory][Blog] [Picking G value]Next Bob and Alice will generate two random numbers (X and Y), calculate an X value and a Y value, respectively:
Diffie-hellman Calculator
| Bob's X Value | Alice's Y value |
| Bob's random value | Alice's random value |
| Bob's A value | Alice's B value |
| A=G^x mod N | B=G^y mod N |
Diffie Hellman Key Exchange Calculator
and Bob will send his A value to Alice, and Alice will send her B value to Bob, and they now re-calculate the values to generate the same shared key:
Diffie-hellman Calculator
| Bob's Key | Alice's Key |
| Key=B^x mod N | Key=A^y mod N |